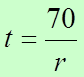Técnicas aplicadas al cambio de la población y sus variantes
Cambio Porcentual de la Población
El cambio que puede ocurrir en un período dado puede reflejar un aumento o una disminución. El interés de este método es establecer cuánto representa porcentualmente este cambio. Permite determinar en cuánto por ciento ha mermado (o aumentado) un fenómeno entre dos puntos de referencia. Al computar la tasa de cambio o por ciento de cambio comparamos el cambio real entre el evento más reciente en un tiempo ƒa contra el evento menos reciente en otro tiempo ƒb, sirviendo como base el evento menos reciente tiempo ƒb. La fórmula estaría expresada de la siguiente manera:
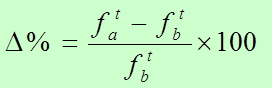
Crecimiento Natural
También conocido como crecimiento vegetativo, saldo natural o saldo vegetativo. Es el aumento natural es el excedente (o déficit) de nacimientos sobre las defunciones en una población durante un período determinado. La fórmula estaría expresada de la siguiente manera:
![]()
Tasa de Crecimiento Aritmética
También conocido como tasa de crecimiento lineal, es el más simple de todos, supone que la población tiene un comportamiento lineal y por ende, la razón de cambio se supone constante donde se incrementa en la misma cantidad cada unidad de tiempo considerada.
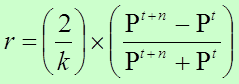
o
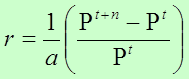
o
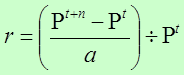
Tasa de Crecimiento Geométrico
También conocido como interés compuesto, esta tasa supone un crecimiento porcentual constante en el tiempo. A diferencia del modelo anterior, dicha tasa mantiene constante el porcentaje de crecimiento por unidad de tiempo y no el monto (cantidad) por unidad de tiempo, por tanto, se puede usar para períodos largos.
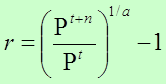
o
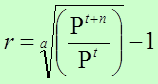
Tasa de Crecimiento Geometrico Simplificado de Bocaz
Otro método para obtener la tasa de crecimiento geométrico es evitando el uso de los logaritmos y cuando el período de tiempo no es muy largo (5 a 10 años), se sugiere la utilización de la expresión simplificada de Albino-Bocaz, veamos:
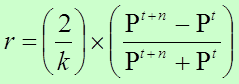
Tasa de Crecimiento Exponencial
A diferencia del modelo geométrico el modelo exponencial supone que el crecimiento se produce en forma continua y no cada unidad de tiempo.
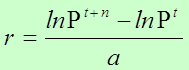
o
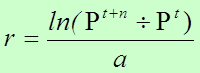
o
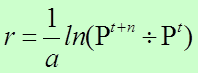
Tiempo de Duplicación
El crecimiento expresado como porcentaje no siempre es muy informativo. ¿Es acelerada o lenta una tasa de crecimiento del tres por ciento? A veces, la forma más gráfica de representar el crecimiento de la población consiste en calcular cuántos años, a su ritmo actual de crecimiento, tardaría en duplicarse una población. Un país con una tasa de crecimiento constante de un uno por ciento duplicaría su población en 70 años, con un dos por ciento, en 35 años; con un tres por ciento, en 23 años.
El tiempo de duplicación es, a lo sumo, una forma aproximada de estimar la futura dimensión de la población. Al calcular el tiempo de duplicación, se obtiene una idea de la rapidez a la que la población crece actualmente. Los métodos más simples consisten en suponer, que el crecimiento de la población sigue un modelo matemático. Para aplicar el método se requiere conocer la tasa de crecimiento de la población y suponer que permanece constante en el futuro. Bajo estos supuestos la determinación del tiempo de duplicación se obtiene de la siguiente manera: