Técnicas aplicadas a la composicion de la población y sus variantes

 

Por Ciento de Hombres

La expresión “por ciento” viene de la frase latina “per centum”, y de ella se deriva la palabra “porcentaje”.  Un sinónimo para expresar el por ciento es distribución porcentual.  Compara el número de casos en una categoría de interés de una variable específica  (hombres) con el tamaño total de la distribución de los casos de todas las categorías, incluyendo la categoría de interés (hombres + mujeres).  Hay que resaltar que los casos de dicha categoría de interés formarán parte del número total de casos en la distribución total. La notación expresada podría ser representada por las siguientes ecuaciones:

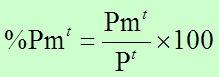
El número de hombres por cada 100 habitantes

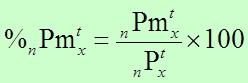
El número de hombres por cada 100 habitantes

 

Por Ciento de Mujeres

Compara el número de casos en una categoría de interés de una variable específica  (mujeres) con el tamaño total de la distribución de los casos de todas las categorías, incluyendo la categoría de interés (mujeres  +  hombres).  La notación expresada podría ser representada por las siguientes ecuaciones:

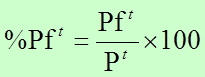El número de mujeres por cada 100 habitantes

 

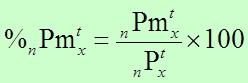
El número de mujeres de x edad por cada 100 habitantes de x edad

Razón de Masculinidad

También conocido como razón por sexo o índice de masculinidad, se utiliza para estimar la relación entre el número de hombres y el de mujeres en una población. Por lo común se expresa como el número de varones por cada 100 mujeres. En la mayoría de los países, el índice de masculinidad al nacer es de aproximadamente 105 varones por cada 100 mujeres. Después del nacimiento, los índices de masculinidad por edades varían conforme se avanza en la edad.

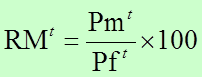
El índice de masculinidad al momento de nacer

 

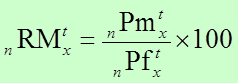
El índice de masculinidad para toda la población y por edad

Edad Mediana

Es el valor que se encuentra en el centro de un conjunto y la misma es fácil de obtener, tanto y cuando las edades estén presentada de forma sencilla y ordenadas. Por consiguiente, es el valor que divide la población o la muestra en dos parte iguales; de tal forma que la mitad de los valores son mayores que la mediana y la otra mitad es menor que la mediana.  Una de las cualidades de esta medida es que los valores extremos no afectan el resultado. Además, es más variable que la edad media pero es menos sensible a los cambios estructurales propios de cada población. Cuando la edades están reagrupadas la mediana debe obtenerse mediante el calculo:

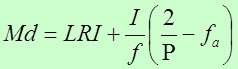
El envejecimiento de la población es constituido por un cambio en la distribución de la población de un país hacia mayores edades. Uno de los indicadores que puede reflejar dicho cambio es la edad mediana.  Se ha establecido que una población con una mediana de edad de 20 años o menos se considera joven; una población con una edad mediana entre 20 a 29 años se considera que esta en transición y una población con una mediana que supere los 30 años es considerada vieja.

 

Edad Media o Promedio

Es la medida de posición central más utilizada, la más conocida y la más sencilla de calcular.   Es el centro de gravedad, el punto alrededor del cual los valores se aglutinan. Su principal desventaja radica en su sensibilidad al cambio de uno de sus valores o a los valores extremos demasiado grandes o pequeños. La media se define como la suma de todos los valores observados, dividido por el número total de observaciones.

Cuando los valores representan una población la ecuación se define como

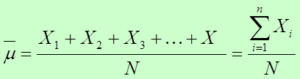
Cuando los valores representan una muestra la ecuación se define como

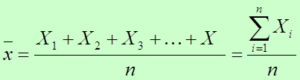
Esta fórmula únicamente es aplicable si los datos se encuentran desagrupados; en caso contrario debemos calcular la media mediante la multiplicación de los diferentes valores por la frecuencia con que se encuentren dentro de la información; es decir:

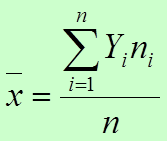
Es importante resaltar que existe una gran variedad de medias como la Media geométrica, la Media ponderada, la Media cuadrática, etc. Por el momento sólo hacemos énfasis en la media aritmética ya que es la más utilizada, aunque se recomienda a los lectores profundizar en estos temas.

 

Índice de Whipple

El Índice de Whipple WI  (índice de concentración de edades) mide la declaración de la edad, respecto a la preferencia hacia ciertos dígitos (0 y 5). En su versión original el Índice de Whipple fue destinado a medir la preferencia o la concentración de población en edades terminadas en los dígitos 0 y 5 respectivamente, sin embargo el método puede ser adaptado para establecer el nivel de atracción por cualquier dígito.

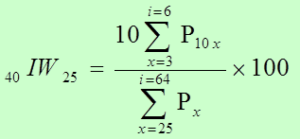
Para el dígito 0

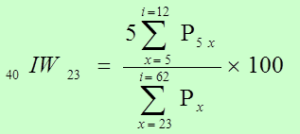
Para los dígitos 0 y 5